
Image source: https://en.bitcoin.it/
A public peer to peer ledger that keeps track of how much each party owns of the native unit of account bitcoin. It was invented in 2009 by an anonymous party (or parties) holding the name Satoshi Nakamato. The first transaction on the bitcoin blockchain encodes the following message: "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks". This message was in reference to an article posted in a british newspaper on 03/Jan/2009.
# This code connects to a bitcoin node (hosted on https://mempool.space)
# holding the full bitcoin blockchain and
# extracts the first message encoded in the genesis block of
# the coinbase transaction.
import requests
from binascii import unhexlify
# getting the block id for the genesis block (block 0).
genesis_block_id = requests.get('https://mempool.space/api/block-height/0').text
# getting all the block transactions of block 0 and parsing it
response = requests.get('https://mempool.space/api/block/' + genesis_block_id + '/txs')
# decode the special message in the genesis block
print(unhexlify(response.json()[0]['vin'][0]['scriptsig_asm'].split(" ")[5]).decode('utf-8'))
The Times 03/Jan/2009 Chancellor on brink of second bailout for banks

Image source: https://en.bitcoin.it/
Definition. A digital signature contains three algorithms:
true or falseAll three algorithms should be efficiently computable. Moreover, the digital signature must satisfy two guarantees: correctness and unforgeability.
Definition. A hash function $H: \{0, 1\}^* \to \{0, 1\}^n$ is an efficiently-computable function that accepts unbounded input and provides output strings of a fixed number of bits $n$.
One wayness: given $y = H(x)$, it is practically infeasible for anyone to find any preimage $x'$ such that $H(x') = y$.
Collision resistance: it is practically infeasible for anyone to find two different inputs $x_1$ and $x_2$ such that $H(x) = H(x')$.
Random oracle: $H$ acts like a randomly-generated truth table would.
If an adversary [Mallory] has not explicitly queried the oracles on some point $x$, then the value of $H(x)$ is completely random... at least as far as [Mallory] is concerned.
– Jon Katz and Yehuda Lindell, Introduction to Modern Cryptography
(Note: any modification to x will lead to a different hash)

Source: Wikipedia
A ledger is a book or collection of accounts in which account transactions are recorded. Each account has an opening or carry-forward balance, and would record each transaction as either a debit or credit in separate columns, and the ending or closing balance.
For every debit recorded in a ledger, there must be a corresponding credit, so that the debits equal the credits in the grand totals. Source Wikipedia
The bitcoin ledger is maintained by everyone running the bitcoin software. Anyone can run the bitcoin software on their computer. All parties are in an agreement over this ledger and the transactions within this ledger. We call these parties nodes.
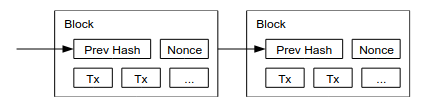
The ledger is seperated into blocks. Each block can contain a number of transactions and always references the hash of the previous block. A block gets added to the blockchain approximately every 10 minutes.
Here is a screenshot of some blocks that were mined yesterday (and one that is not the process of being so). I took these pictures using a blockchain explorer. Note that anyone can run a node and install a blockchain explorer.
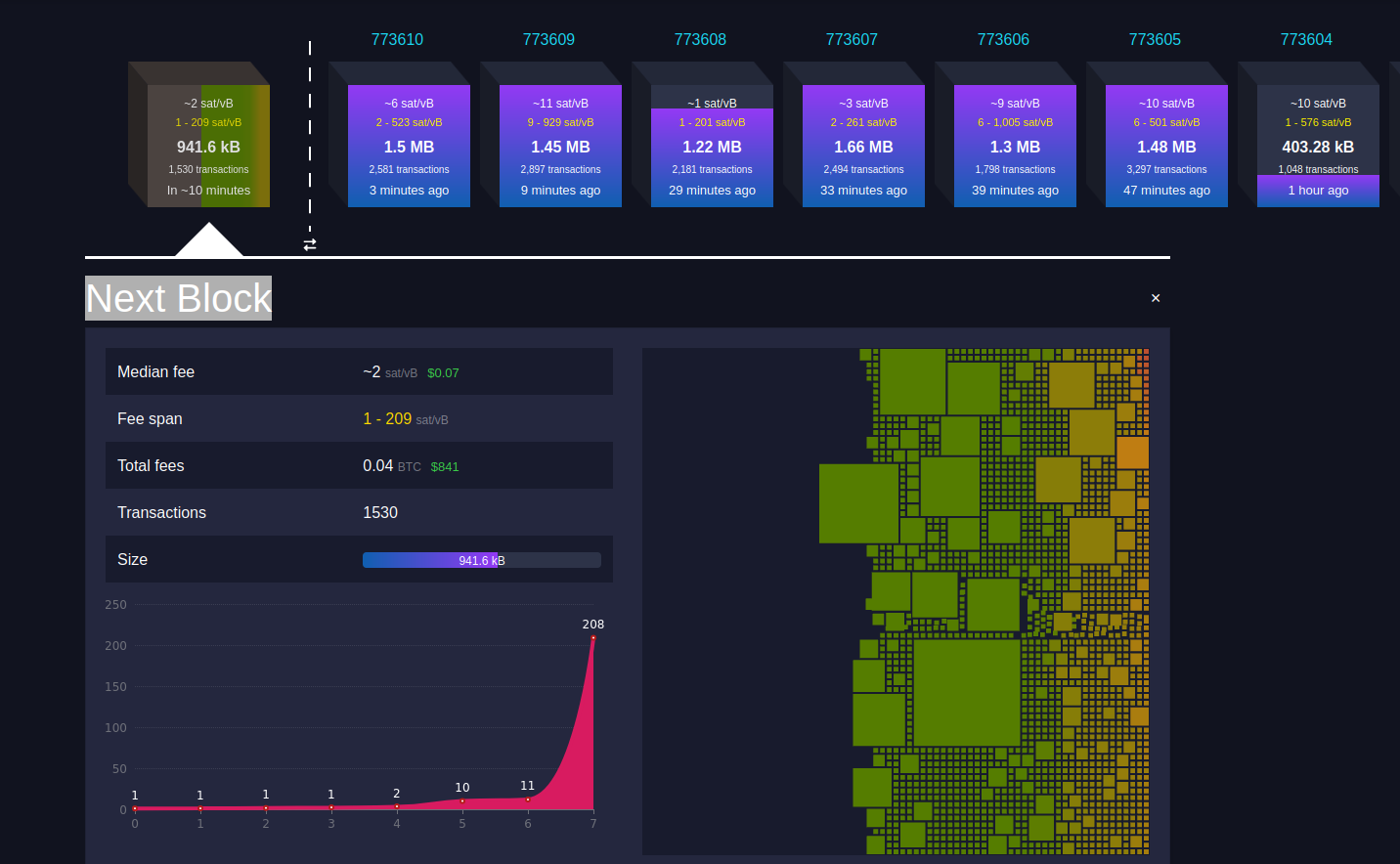
In this screenshot there is a bitcoin address with approx 3.22BTC sending approx 0.049BTC to one address and 3.17BTC to another.

# Every block references the previous block
# getting block 773610 that is in the screenshot
import requests
from binascii import unhexlify
# getting the block hash of 773610
block_hash = requests.get('https://mempool.space/api/block-height/773610').text
# get block metadata
response = requests.get('https://mempool.space/api/block/' + block_hash)
print(response.json()['previousblockhash'])
00000000000000000004574d28ac29cd49708820c68dd09d8bd88ed8bf1a341b
If one were to edit one transaction of a specific block they will also have to edit every block that comes after that block. This is because every future block is pointing to the hash of the previous block.
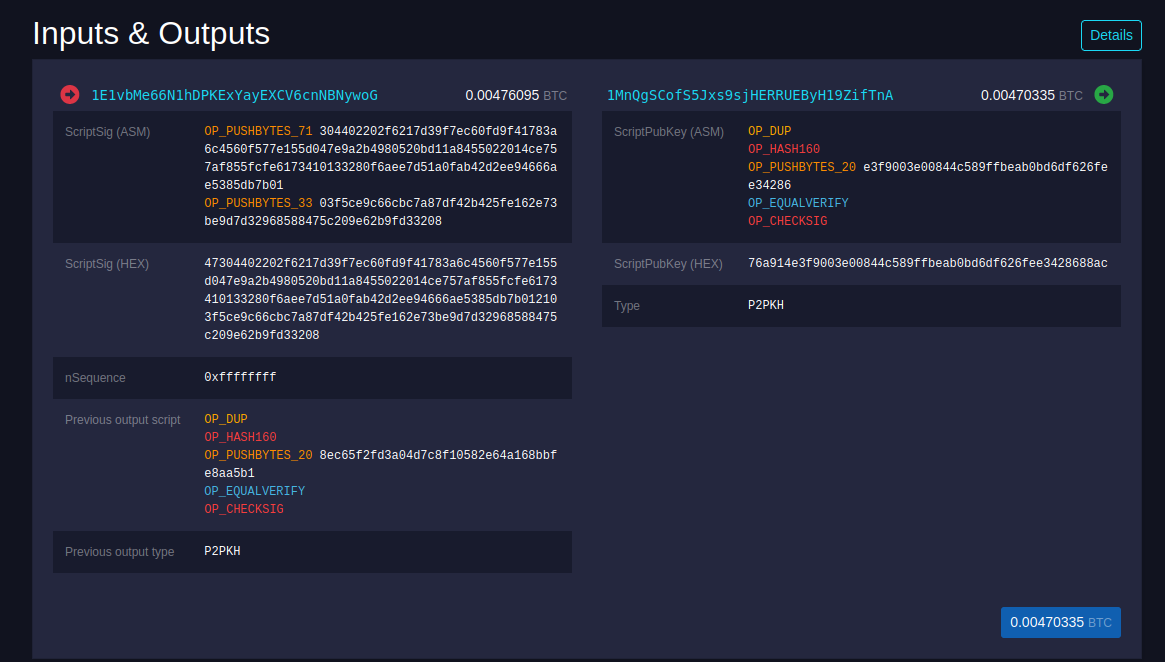
For a transaction to be valid, the sender of the transaction must specifiy where they got their coins from. Also, the sender shouldn't be sending more than what they have. What goes out must be less than or equal to what goes in. If $in \ge out$, the amount $in-out$ is considered fees and a miner can claim the money for themself. Else the transaction is considered invalid.
A bitcoin address is computed from a public key. In the below snippet of code, we are creating an actual bitcoin address right now!
!pip install "cryptos @ git+https://github.com/nicolas3355/cryptos"
from cryptos.keys import gen_secret_key, PublicKey
from cryptos.bitcoin import BITCOIN
# generate a secret/public key pair
secret_key = gen_secret_key(BITCOIN.gen.n)
public_key = PublicKey.from_sk(secret_key)
print('generated secret key:')
print(hex(secret_key))
print('corresponding public key:')
print(public_key)
# get the associated bitcoin address
addr = public_key.address(net='main', compressed=True)
print('compressed bitcoin address (b58check format):')
print(addr)
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/ Collecting cryptos@ git+https://github.com/nicolas3355/cryptos Cloning https://github.com/nicolas3355/cryptos to /tmp/pip-install-8whna9ik/cryptos_e66739370806414c951bac11f8da58d0 Running command git clone --filter=blob:none --quiet https://github.com/nicolas3355/cryptos /tmp/pip-install-8whna9ik/cryptos_e66739370806414c951bac11f8da58d0 Resolved https://github.com/nicolas3355/cryptos to commit 4e01811d449e0292ffb2ac08f7a49a43ffa9cceb Preparing metadata (setup.py) ... done Building wheels for collected packages: cryptos Building wheel for cryptos (setup.py) ... done Created wheel for cryptos: filename=cryptos-1.0-py3-none-any.whl size=22965 sha256=fc5522154aa5b486ca4ac2804e06e593b2764ea493a5694b83442fbff0562aeb Stored in directory: /tmp/pip-ephem-wheel-cache-wvjt2zea/wheels/7d/3f/14/44c1d38124ec0668722a79bc0718762cb538bf24f6c95aabc4 Successfully built cryptos Installing collected packages: cryptos Successfully installed cryptos-1.0 generated secret key: 0x7a3e8bfa09e6ceb36cebe84b2ad2181f8996ccb969326a0dc9677df2468d37eb corresponding public key: PublicKey(curve=Curve(p=115792089237316195423570985008687907853269984665640564039457584007908834671663, a=0, b=7), x=103016115360421655342945202929628046207358169868085253813782939278876286995237, y=94982696061610089227674092825845224192632594785648011908165719440875631939648) compressed bitcoin address (b58check format): 12rgNEcxjTxJRAifSi7yDyGshhKAUT15v9
A bitcoin address spending their (unspent) output by having it as an input to another transaction. The spender is providing a public key and a valid digital signature. The hash of the public key must be $8ec...b1$. All nodes verify that the signature is valid and that the sender has enough money to spend.
Assume you have a job opening and there are millions of applicants. You can't handle this huge number. What do you do?
In this part we are going to talk about two problems that the bitcoin network has solved using proof of work:
In order to understand these two parts, we are going to revist the random oracle property of a hash function. For any new input, the hash function should behave like a random Oracle and it should return a uniformly random output. Given a new input x, each bit in h(x) (whether 0 or 1) should be equally likely to appear.
# what is the probability that when I hash a random string, I get a hash that starts with 4 bits that are all zeroes?
from hashlib import sha256
import os
# count = 0
# hash = "1"
# #note that when working with hexadecimals each digit is 4 bits.
# while(hash[0] != '0'):
# count += 1
# hash = sha256(os.urandom(32)).hexdigest()
# print(hash)
# print(count)
# running the trial a 100 times
arr = []
nb_of_trials = 100
for _ in range(0, 100):
count = 0
hash = "1"
while(hash[0] != '0'):
count += 1
hash = sha256(os.urandom(32)).hexdigest()
arr.append(count)
print(sum(arr)/100)
16.6
# let's increase the number of zeroes and see what happens
from hashlib import sha256
import os
arr = []
nb_of_trials = 100
for _ in range(0, 100):
count = 0
hash = "1"
while(hash[0:4] != '0'*4):
count += 1
hash = sha256(os.urandom(32)).hexdigest()
arr.append(count)
print(sum(arr)/100)
66033.0
Whenever we add a '0' in bits (not in hex), we increase the difficulty of finding such a hash by exactly 2. As we will see later bitcoin uses a variation of this to do mining! However, bitcoin does so while increasing the difficulty in a smoother way. You can read more about it here.
#Looking at block 773610 again
import requests
from binascii import unhexlify
# getting the block hash of block number 773610
block_hash = requests.get('https://mempool.space/api/block-height/773610').text
# geting block metadata
response = requests.get('https://mempool.space/api/block/' + block_hash)
print(response.json())
{'id': '0000000000000000000456ef87595d6674db29d43010345de5f372445cf9b6b1', 'height': 773610, 'version': 536895488, 'timestamp': 1674686421, 'tx_count': 2581, 'size': 1496003, 'weight': 3993173, 'merkle_root': '644550e8b7946910572e18b9872342a56c3ad9e4691cf7b9be7f7c8e9e76acbb', 'previousblockhash': '00000000000000000004574d28ac29cd49708820c68dd09d8bd88ed8bf1a341b', 'mediantime': 1674683784, 'nonce': 885853051, 'bits': 386366690, 'difficulty': 37590453655497}
You can see that the id of the block starts with a lot of zeroes! Bitcoin uses the property of hashes to do what we call leader election. Every party in the bitcoin network can compete over the right to add a block to the blockchain. However, the block hash has to meet some difficulty level. The first party to find such a block, earns the right to become a leader and put the next block in the blockchain.

If miners start finding blocks too fast (on average). The difficulty of finding a block increases.
If miners start finding blocks too slowly (on average). The difficulty of finding a block decreases.