Lab 2: Encoding.

1. Information as numbers.
2. Different ways of encoding numbers: Base-1(Unary), Base-2(Binary), ..., Base-10(Decimal), ... base-16(Hex).
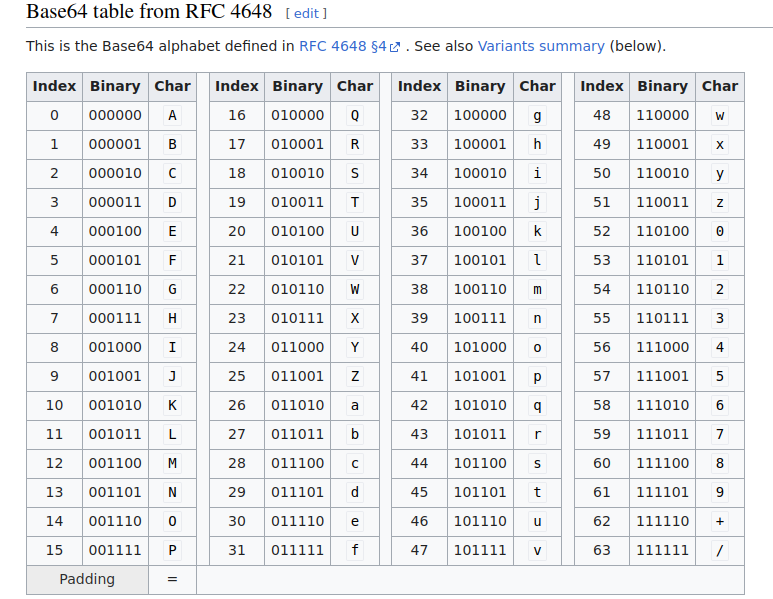
3. Binary-to-text encoding: Hex, Ascii table, Base-32/58/64.

Information as numbers.

When person A sends information to person B. A is referencing a specific state in the context of possible states between A and B. If the states are ordered, then for A to send information to B, it suffices for A to send a number to B.

In the following examples can you think of how we can use numbers and context to relay the information we need?

• Pointing

• A flare gun can be used to either encode the location of a person or the start of a race among other things. If one sees a flare gun in the middle of a nowhere then it's probably someone missing... (can you think of other ways you can send information using a flare gun).

• An English word.
• An image.

Everything can be considered information, and information can be encoded as numbers. This applies not only to computing, but also to biology, where DNA serves as a code that encodes genetic information.

Encoding numbers

Unary (base-1)

Unary numbers only have 1 digit. The simplest way of representing numbers:

Decimal numbers (base-10)

We humans like decimal numbers. We have ten fingers. Counting is easy when we can link them to something physical. It's called base-10 because there are ten digits. For numbers bigger than 9 we re-use the digits we already have.

Hexadecimal numbers (base-16)

Hexadecimal numbers have 16 digits: 0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f. If we need to reference a number bigger than 15, we also re-use the digits that we already have (just like base-10). For example, \x11 represents number 17 (in decimal). Note: We use \x in front of a number to denote that it's a hexadcimal number.

Binary numbers (base-2)

Binary numbers have only 2 digits: 0 and 1. If we need to reference a number bigger than 1, we also re-use the digits that we already have. For example, 11 represents number 3 (in decimal).

While there have been computers that use number systems other than binary, binary is the most widely used and dominant number system in modern computing due to its simplicity, scalability, and compatibility with the underlying electronics of computers.

Electronics: Binary is well-suited to the underlying electronics of computers, as it maps directly to the two voltage levels (high and low) used in electronic switches.

Memory and storage: Binary can be used to store and retrieve data in a compact and efficient manner, as each binary digit (or "bit") represents a single binary value (0 or 1).

Binary to text encoding

When trying to convey info to people (or generally outputting it as a string) we need to find an efficient and understandable way of doing so. Binary is not a good way for us humans to understand things.

For example: assuming the least significant bit is on the right, what is the decimal number corresponding to 101111011 ?

print(2**0 + 2**1 + 2**3 + 2**4 + 2**5 + 2**6+ 2**8)

print(int('101111011', 2))

379
379

# we use the bin command to look at the binary representation of a decimal number
bin(379)

'0b101111011'

Hexadecimal encoding of binary

What about the hex representation of 01111011?

hex(int('100111011', 2))

'0x13b'

It's now easier to interpret the binary number "100111011". We split the big binary number into chunks, each chunk is of size 4 bits. We can now interpret each chunk at a time.

When we print random bytes in python. Python sometimes prints the hexadecimal representation of the byte.

import os

# generating 32 random byte
r = os.urandom(32)
print(r)

b'\xe8\x1f\x14\x10\x12\x16&U\xe9\xdf\xbf^\x1d\xcf\xb1J\xbf]1&?%\xc1)\x03\xf5\xc5\x90 \x11A\x9b'

Why bytes not bits?

Programming languages use bytes as a unit of measurement for memory because bytes are more convenient for measuring memory than bits. Bytes are multiples of 8 bits and can easily be used to store a character or number in a single unit, which makes it easier to manipulate data stored in memory. On the other hand, using bits would be more difficult and less efficient for memory storage and manipulation.

While hexadecimals maybe a good way for us to interpret binary encoding numbers it is not the best way to understand text!

ASCII encoding of binary

ASCII encoding is 7 bits long.

Printable ASCII characters.

Binary Oct Dec Hex Glyph 1963 1965 1967 010 0000 040 32 20  space 010 0001 041 33 21 ! 010 0010 042 34 22 " 010 0011 043 35 23 # 010 0100 044 36 24 $ 010 0101 045 37 25 % 010 0110 046 38 26 & 010 0111 047 39 27 ' 010 1000 050 40 28 ( 010 1001 051 41 29 ) 010 1010 052 42 2A * 010 1011 053 43 2B + 010 1100 054 44 2C , 010 1101 055 45 2D - 010 1110 056 46 2E . 010 1111 057 47 2F / 011 0000 060 48 30 0 011 0001 061 49 31 1 011 0010 062 50 32 2 011 0011 063 51 33 3 011 0100 064 52 34 4 011 0101 065 53 35 5 011 0110 066 54 36 6 011 0111 067 55 37 7 011 1000 070 56 38 8 011 1001 071 57 39 9 011 1010 072 58 3A : 011 1011 073 59 3B ; 011 1100 074 60 3C < 011 1101 075 61 3D = 011 1110 076 62 3E > 011 1111 077 63 3F ? 100 0000 100 64 40 @ ` @ 100 0001 101 65 41 A 100 0010 102 66 42 B 100 0011 103 67 43 C 100 0100 104 68 44 D 100 0101 105 69 45 E 100 0110 106 70 46 F 100 0111 107 71 47 G 100 1000 110 72 48 H 100 1001 111 73 49 I 100 1010 112 74 4A J 100 1011 113 75 4B K 100 1100 114 76 4C L 100 1101 115 77 4D M 100 1110 116 78 4E N 100 1111 117 79 4F O 101 0000 120 80 50 P 101 0001 121 81 51 Q 101 0010 122 82 52 R 101 0011 123 83 53 S 101 0100 124 84 54 T 101 0101 125 85 55 U 101 0110 126 86 56 V 101 0111 127 87 57 W 101 1000 130 88 58 X 101 1001 131 89 59 Y 101 1010 132 90 5A Z 101 1011 133 91 5B [ 101 1100 134 92 5C \ ~ \ 101 1101 135 93 5D ] 101 1110 136 94 5E ↑ ^ 101 1111 137 95 5F ← _ 110 0000 140 96 60 @ ` 110 0001 141 97 61 a 110 0010 142 98 62 b 110 0011 143 99 63 c 110 0100 144 100 64 d 110 0101 145 101 65 e 110 0110 146 102 66 f 110 0111 147 103 67 g 110 1000 150 104 68 h 110 1001 151 105 69 i 110 1010 152 106 6A j 110 1011 153 107 6B k 110 1100 154 108 6C l 110 1101 155 109 6D m 110 1110 156 110 6E n 110 1111 157 111 6F o 111 0000 160 112 70 p 111 0001 161 113 71 q 111 0010 162 114 72 r 111 0011 163 115 73 s 111 0100 164 116 74 t 111 0101 165 117 75 u 111 0110 166 118 76 v 111 0111 167 119 77 w 111 1000 170 120 78 x 111 1001 171 121 79 y 111 1010 172 122 7A z 111 1011 173 123 7B { 111 1100 174 124 7C ACK ¬ | 111 1101 175 125 7D } 111 1110 176 126 7E ESC | ~

# let's look at the byte of the character z
print(b'z')

b'z'

from binascii import hexlify

print(hexlify(b'z'))

b'7a'

Binary Oct Dec Hex Abbreviation Unicode Control Pictures^[b] Caret notation^[c] C escape sequence^[d] Name (1967) 1963 1965 1967 000 0000 000 0 00 NULL NUL ␀ ^@ \0 Null 000 0001 001 1 01 SOM SOH ␁ ^A Start of Heading 000 0010 002 2 02 EOA STX ␂ ^B Start of Text 000 0011 003 3 03 EOM ETX ␃ ^C End of Text 000 0100 004 4 04 EOT ␄ ^D End of Transmission 000 0101 005 5 05 WRU ENQ ␅ ^E Enquiry 000 0110 006 6 06 RU ACK ␆ ^F Acknowledgement 000 0111 007 7 07 BELL BEL ␇ ^G \a Bell 000 1000 010 8 08 FE0 BS ␈ ^H \b Backspace^[e][f] 000 1001 011 9 09 HT/SK HT ␉ ^I \t Horizontal Tab^[g] 000 1010 012 10 0A LF ␊ ^J \n Line Feed 000 1011 013 11 0B VTAB VT ␋ ^K \v Vertical Tab 000 1100 014 12 0C FF ␌ ^L \f Form Feed 000 1101 015 13 0D CR ␍ ^M \r Carriage Return^[h] 000 1110 016 14 0E SO ␎ ^N Shift Out 000 1111 017 15 0F SI ␏ ^O Shift In 001 0000 020 16 10 DC0 DLE ␐ ^P Data Link Escape 001 0001 021 17 11 DC1 ␑ ^Q Device Control 1 (often XON) 001 0010 022 18 12 DC2 ␒ ^R Device Control 2 001 0011 023 19 13 DC3 ␓ ^S Device Control 3 (often XOFF) 001 0100 024 20 14 DC4 ␔ ^T Device Control 4 001 0101 025 21 15 ERR NAK ␕ ^U Negative Acknowledgement 001 0110 026 22 16 SYNC SYN ␖ ^V Synchronous Idle 001 0111 027 23 17 LEM ETB ␗ ^W End of Transmission Block 001 1000 030 24 18 S0 CAN ␘ ^X Cancel 001 1001 031 25 19 S1 EM ␙ ^Y End of Medium 001 1010 032 26 1A S2 SS SUB ␚ ^Z Substitute 001 1011 033 27 1B S3 ESC ␛ ^[ \e^[i] Escape^[j] 001 1100 034 28 1C S4 FS ␜ ^\ File Separator 001 1101 035 29 1D S5 GS ␝ ^] Group Separator 001 1110 036 30 1E S6 RS ␞ ^^^[k] Record Separator 001 1111 037 31 1F S7 US ␟ ^_ Unit Separator 111 1111 177 127 7F DEL ␡ ^? Delete^[l][f]

# let's print some invisible ascii characters 
# i will pick the tab

print('\t hello')

 hello

from binascii import hexlify
a = '\t'.encode('ascii')
print(hexlify(a))
print(a)

b'09'
b'\t'

#Let's write hello in ascii bytes
# a = b'hello'
a = [104, 101, 108, 108, 111]
print(a)
print(bytes(a))
# let's add a new line
a.append(0x0A)
print(bytes(a))
print(bytes(a).decode('ascii'))

[104, 101, 108, 108, 111]
b'hello'
b'hello\n'
hello

What happens when we try to print something outside the range of ASCII? ASCII is 7 bits but a byte is 8 bits.

print(bytes([104,255]))

b'h\xff'

Using ASCII each character costs exactly 7 bits to encode. Can we reduce it more? Can we have 6 bits per character?

BASE-64 encoding

The answer to that question is yes but at the expense of expressibility. Base64 provides a more efficient encoding method compared to ASCII as each Base64 character can represent 6 bits of data while ASCII can represent only 7 bits.

import base64
a = base64.b64decode('helloooo')
print(hexlify(a))
print(len(a))
a = b'helloooo'
print(hexlify(a))
print(a)

b'85e965a28a28'
6
b'68656c6c6f6f6f6f'
b'helloooo'

"Base64 is designed to carry data stored in binary formats across channels that only reliably support text content. Base64 is particularly prevalent on the World Wide Web where one of its uses is the ability to embed image files or other binary assets inside textual assets such as HTML and CSS files.

Base64 is also widely used for sending e-mail attachments. This is required because SMTP – in its original form – was designed to transport 7-bit ASCII characters only. This encoding causes an overhead of 33–37% (33% by the encoding itself; up to 4% more by the inserted line breaks)." Source: wikipedia

import os
import base64

r = os.urandom(32)
print(len(r))
try:
  print(r.decode('ascii'))
except Exception as e:
  print(e)

b64encoded = base64.b64encode(r)
print(b64encoded)
print(len(b64encoded))
print(base64.b64decode(b64encoded))
print(len(b64encoded)/len(r))

32
'ascii' codec can't decode byte 0xa8 in position 0: ordinal not in range(128)
b'qE2A0WSQbAa6Fd+HCms53iSVP118gGMvJgoFBxTMYE0='
44
b'\xa8M\x80\xd1d\x90l\x06\xba\x15\xdf\x87\nk9\xde$\x95?]|\x80c/&\n\x05\x07\x14\xcc`M'
1.375