Source:Wikipedia
[Note: this lecture is based on material in Elaine Shi's textbook in chapters 5, 6, 12, and 13.]
In the last few lectures, we studied the Byzantine Broadcast problem. In this question:
There are a total of $n$ parties, including the sender. Within the group, there is a subset of $f$ generals who can be faulty in arbitrarily-malicious ways, including the sender.
These protocols can be constructed for different types of networks.
Bounded vs unbounded delay:
Network setup:
We introduced two protocols in the synchronous setting:
Then we introduced one protocol in the asynchronous setting: Bracha's broadcast.
| Dolev-Strong |
Phase-King |
Bracha broadcast |
|
|---|---|---|---|
| PKI | YES |
NO | NO |
| Synchronous network |
YES | YES | NO |
| Number of fauly parties |
f ≤ n - 2 | f ≤ (n-1)/(3) | f ≤ (n-1)/(3) |
| Number of rounds |
f+1 | 3(f+1) | constant |
| Guaranteed termination? |
YES | YES | NO |
Byzantine Broadcast protocols guarantee the following properties.
Throughout this course, our security guarantees only protect the honest parties. That's because we have no idea what the corrupted parties will do; we can't stop them from taking a different action nor can we protect one corrupted party from another corrupted party.
One exception here: in the asynchronous setting, we do not require termination because it is impossible to achieve. In particular:
In the last lecture, we learned that common randomness is a very powerful tool to have when designing distributed systems protocols. As an example of the power of common randomness, we reduced the number of rounds of the phase king protocol from $3(f+1)$ rounds to a constant number of rounds $k$.
The randomized phase-king protocol had the following structure.
The main idea was that with high probability we are going to have at least one honest leader that will broadcast the right value to everyone.
To use common randomness we assumed that a common coin protocol already existed. We imagined that the $n$ parties can get together to flip a coin. The common coin had the following properties:
Note that we can easily extend from 1 bit (or coin flip) to more bits (or more coin flips) by running multiple instances of our common coin protocol.
In this lecture, we are going to look at the problem of creating common randomness. But first we are going to look at yet another use case for common randomness.
In that last lecture we learned that we can use byzantine broadcast to build a permissioned blockchain. Can we use asynchronous byzantine broadacast to build a permissioned blockchain in the asynchronous setting?
Actually, this doesn't quite work. Do you see why?
The problem is that Bracha's broadcast protocol doesn't guarantee termination.
As a result, we may never be certain when the epoch where Party 1 is the designated sender has ended, so that we can move on to the next epoch with Party 2 as the designated sender.
At first glance, this looks to be an insurmountable problem.
As we said in the recap at the top of the class, it is actually impossible to build an asynchronous Byzantine Broadcast protocol that guarantees termination. The problem is that the designated sender might simply refuse to participate in the protocol, and the honest parties will wait forever to listen for a message that may never arrive.
In some sense, the problem here stems from the fact that we are putting all of our faith in a single party to serve as the designated sender.
So let's back away from that . We can define a new, slightly more general question called Byzantine Agreement. This is basically the same as Byzantine Broadcast, except that now everyone gets to send a message at the same time.

Source:Wikipedia
Let's modify our properties from Byzantine Broadcast to work in the new setting of Byzantine Agreement.
Agreement is the same as before:
all honest parties decide the same value.
Validity only needs to hold if everyone starts with the same message... or at least, all the honest parties do, since we can never be sure what the faulty parties are doing. Formally, we guarantee that:
if all honest parties start with the same input value, then this shared value is guaranteed to become the decision value.
Liveness is the asynchronous version of what we used to call termination. It states that:
all honest nodes output eventually (assuming that messages are delivered eventually, albeit with arbitrary delays)
In the synchronous setting, there are many ways to build Byzantine Agreement. One simple approach is to run $n$ copies of Byzantine Broadcast in parallel, where everyone is the designated sender in one of them, and then take a majority vote of the results.
This works as long as $f < \frac{n}{2}$, since otherwise the faulty parties are in the majority and can overrule the honest parties' values. (And it turns out that $f < \frac{n}{2}$ is the best that one can do.)
But the asynchronous setting is where things really get interesting. It turns out that:
It is impossible to construct asynchronous Byzantine Agreement, even in the easiest possible setting where there is only $f = 1$ faulty party.
But: using a CommonCoin, it is possible to build asynchronous Byzantine Agreement that can withstand up to $f < \frac{n}{3}$ faulty parties!
In other words, we can achieve liveness with Byzantine Agreement, even though it was impossible to accomplish with Byzantine Broadcast.
Furthermore, we can use Byzantine Agreement as the basis of a blockchain protocol. Rather than asking each party in turn to broadcast a block to add to the log, instead in each epoch everyone can propose a block as input to a Byzantine Agreement protocol and then we can add the agreed-upon block to the log.
(Note that this requires some small modifications to our definition of blockchains so it works in the asynchronous setting. This part is not so bad though; see if you can do that yourself.)
In the rest of this lecture, we will delve into more details about how to build a CommonCoin. In the future, we will also look into how to harness the power of randomness to design blockchains in a new way.
One way we can agree about common randomness is to ask a trusted source. As long as the source is trustworthy and won't collude with the attacker we should be okay.
This is exactly what NIST Randomness Beacon provides. Since September 5th, 2013 the US National Institute of Standards and Technology (NIST) has been publishing a 512-bit, full-entropy random number every minute of every day. Each new post is called a pulse. Here is a link to the latest pulse: "https://beacon.nist.gov/beacon/2.0/pulse/last".
Here is a screenshot of a NIST random beacon pulse:
The pulse contains several fields:
You can read about the full NIST specifications here.
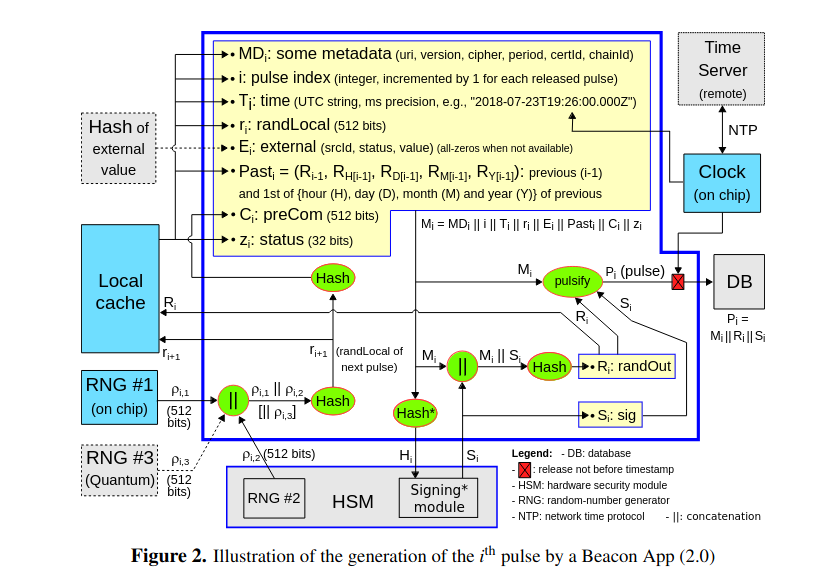
Three independant different sources of randomness feed entropy into each pulse (another source is the state of the previous pulse).
What's wrong with using NIST's random beacon to elect leaders or to pick what restaurents we should go to?
Nothing is wrong as long as you trust NIST. That's why it was build for.
Can NIST cheat? Can you think of a way where they can cheat?
NIST can try to precompute many different output using the randlocals and throw away the outputs that they don't like. Thus they can bias the output.

Let's try to build a common coin between two parties A and B.
Solution: A party can throw the coin while the other party watches.
Potential Solution: Party A sends a video of them throwing the coin to Party B. Party watches the video and gets convinced that Party did indeed throw a coin.
What's wrong with scenario 2?
Party A can bias the output.
The problem with the previous approach was that the final coin output depends only on player A's coin flip. Player A can flip many coins and select the output that they like. What if the final coin output depends on both player A and B's input equally? Can player A still cheat?
The protocol: Party A picks a bit $b_1$ and a secret salt $s$ at random. Party A sends $h = hash(b_1 || s)$ to Party B.
Party B picks a bit $b_2$ at random.
Party A reveals $b_1$ and the salt $s$ to B. Party B checks that Party A told the truth by checking that $h == hash(b|| s)$. If the check is true then the output bit is then $b_1 \oplus b_2$. If the check false, Party B considers Party A to be a cheater and refuses to play with them again.
Let's do it together right now. Here is the hash of a value I personally committed to yesterday f3affea5f3c3b7fcc737981890e326565faad526cf195298fa659a44d41de1f8
import hashlib
salt = b" this is a salt"
b = b"0"
print(hashlib.sha256(b + salt).hexdigest())
f3affea5f3c3b7fcc737981890e326565faad526cf195298fa659a44d41de1f8
Why does this work? Why can't party A or B bias the coin?
The output of the coin depends on the output of both players. Each party's input has an equal impact on the final result. Player A committed to their random value and cannot change it before seeing Player B's value. Similiarly, player B doesn't know what value Player A has chosen because the output of the hash function looks random.
It is crucial for player B not to play again if Player A refuses to send their salt. Otherwise, Player A can always bias the coin by refusing to supply the salt when the output is not in their favor.
We can generalize the commit and reveal method we used in the two party setting to the multi party setting. The Protcol would work in the following way.
A version of this commit and reveal is used in eth2.0 as a source of randomness for the blockchain. The randomness is used to do leader election for block proposers among other things (think applications like lottery). You can read more about it here.
Can you describe an attack over the method that we just discussed?
In Round 2, an attacker would wait for everyone else to send their salt. The attacker would compute the output with and without their own input bit. Based on that result, the attacker would choose to reveal their bit.
Economic solution: Let everyone who wants to participate in the randomness generation send money to a smart contract. They can only get their money back if they completed Round 2.
In case the attacker doesn't reveal their salt properly. The attacker would get slashed and loose money. But what happens if the reward they get from biasing the coin is greater than the reward they have to pay?
Cryptography solution: A better approach is not to rely on the players to reveal their own commitments. Instead, it would be nice if the group of players can reveal any commitment of any single party. That way, no single party can choose not to reveal it's own value.
We will later discuss Multi Party Computation and specifically Verifiable Secret Sharing. This will let a party commit to the bit such that a threshold of the group can open the commitment (even though the original Party that did the commitment might refuse to open it).